The answer has nothing at all to do with the Higgs boson.
In this Universe, there are very few fundamental properties that cannot be derived from something simpler. The rules governing biological systems are rooted in chemical interactions, bonds, and applied voltages. The rules of chemistry can be derived from more fundamental physical laws that govern all particles. And if you strip down the components of any physical system, you’ll eventually arrive at the simplest descriptions of reality we know of: the particles and interactions that make up all of our known reality. While all the particles that exist have their own specific, unique properties, there are only a few that define them, such as mass, electric charge, color charge, and weak hypercharge. Yet why the particles have the properties they do is not fully understood; the values of the fundamental constants behind the Universe cannot be derived from anything presently known.
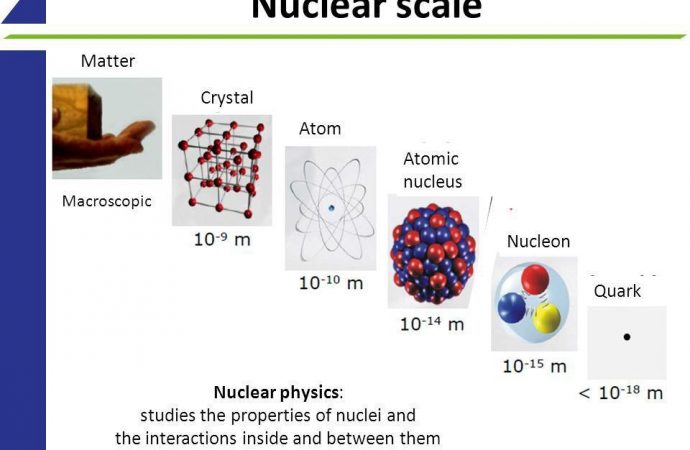
For thousands of years, humanity has searched for the smallest, most fundamental building blocks of nature. Since ancient times, we conjectured that there would be some smallest, uncuttable entities that composed everything in existence. The Greek word ἄτομος, where we get our word “atom” from, literally means indivisible, and yet atoms themselves can be broken up further: into protons, neutrons, and electrons. The electrons are truly uncuttable, but protons and neutrons can be broken up further: into quarks and gluons.
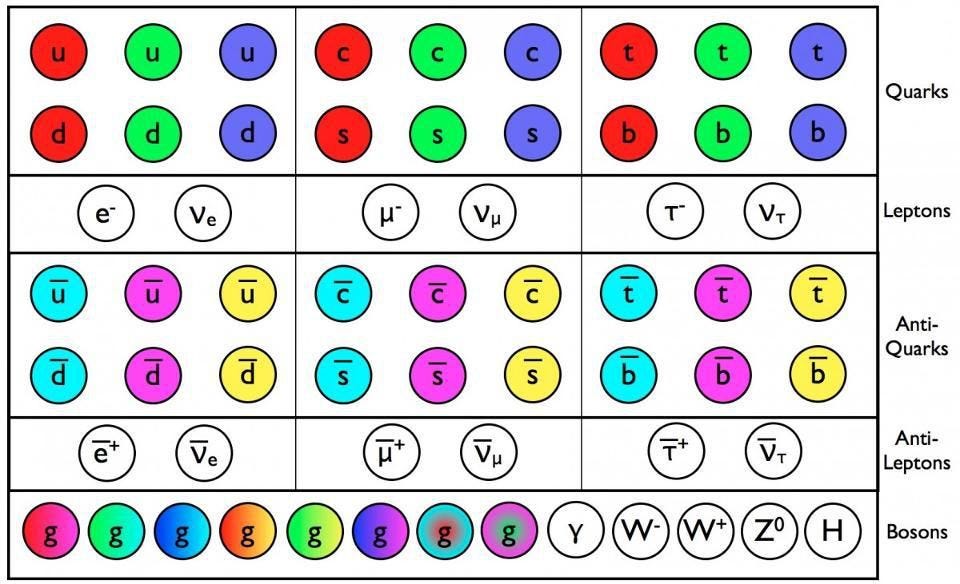
Only here do we arrive at the truly indivisible particles that make up the majority of mass in the world. The particles of the Standard Model — and the ways they bind together — take us to our deepest understanding of reality.
Yet if we take a look at the proton (made of two up and one down quark) and the neutron (made of one up and two down quarks), a puzzle emerges. The three quarks within a proton or neutron, even when you add them all up, comprise less than 0.2% of the known masses of these composite particles. The gluons themselves are massless, while the electrons are less than 0.06% of a proton’s mass. The whole of matter, somehow, weighs much, much more than the sum of its parts.
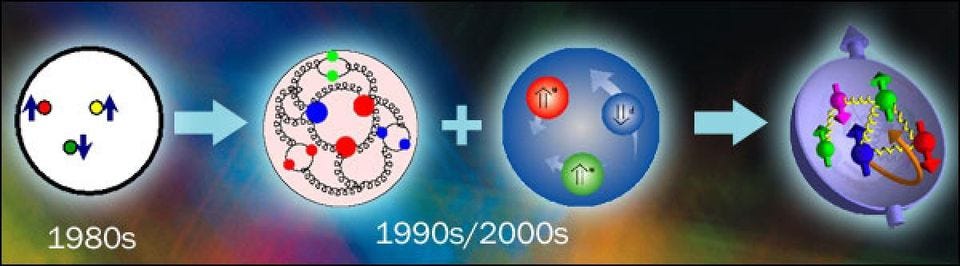
The Higgs may be responsible for the rest mass of these fundamental constituents of matter, but the whole of a single atom is nearly 100 times heavier than the sum of everything known to make it up. The reason has to do with a force that’s very counterintuitive to us: the strong nuclear force. Instead of one type of charge (like gravity, which is always attractive) or two types (the “+” and “-” charges of electromagnetism), the strong force has three color charges (red, green and blue), where the sum of all three charges is colorless.
Furthermore, there are three anti-colors: cyan (anti-red), magenta (anti-green) and yellow (anti-blue), and any color-anticolor combination is also colorless. This is why you can have baryons (made of 3 quarks) or mesons (made of quark/antiquark combinations): because nature needs your complete, bound object to be colorless.
The way quarks bind into protons is fundamentally different from all the other forces and interactions we know of. Instead of the force getting stronger when objects get closer — like the gravitational, electric or magnetic forces — the attractive force goes down to zero when quarks get arbitrarily close. And instead of the force getting weaker when objects get farther away, the force pulling quarks back together gets stronger the farther away they get.
This property of the strong nuclear force is known as asymptotic freedom, and the particles that mediate this force are known as gluons. Somehow, the energy binding the proton together, the other 99.8% of the proton’s mass, comes from these gluons.
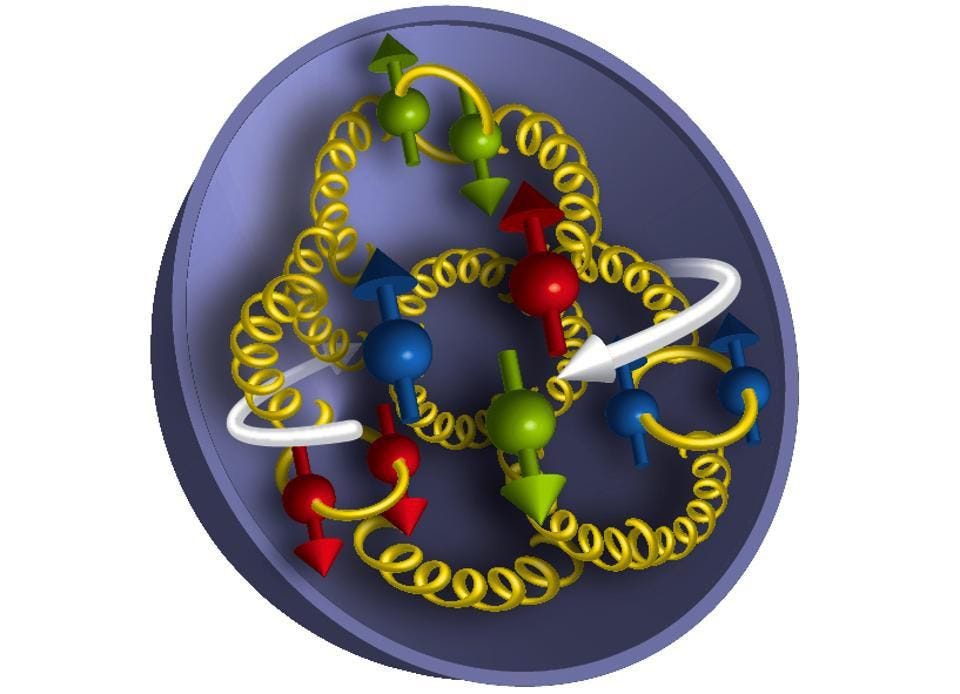
Because of how the strong nuclear force works, there are large uncertainties as to where these gluons are actually located at any point in time. We presently have a solid model of the average gluon density inside a proton, but we need better experimental data and more informed models to know where they are at any particular time.
But even with all the things we don’t know, one puzzle is finally yielding: how to calculate the expected mass of not just the proton, but of all atomic nuclei, based on the quark content alone. The strong nuclear force is responsible for a slew of incredible properties of nature, including:
- how protons and neutrons bind together to make atomic nuclei,
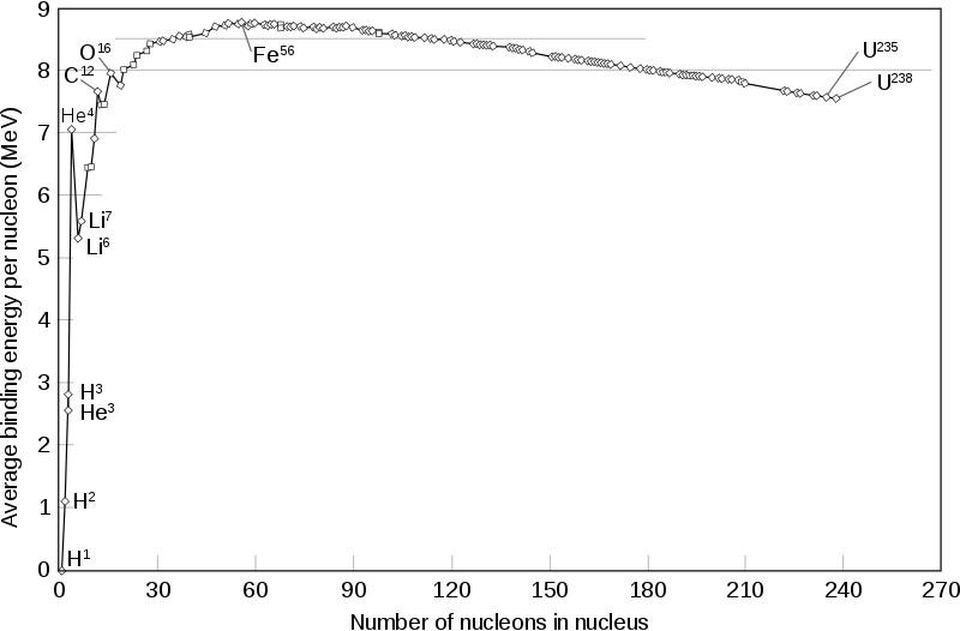
- why different elements have different mass-per-nucleon ratios,
- how and at what rate nuclear reactions in the Sun occur,
- and why iron, nickel and cobalt are the most stable elements.
The difficult part with the quantum field theory that describes the strong force — quantum chromodynamics (QCD) — is that the standard approach we take to doing calculations is no good. Typically, we’d look at the effects of particle couplings: the charged quarks exchange a gluon and that mediates the force. They could exchange gluons in a way that creates a particle-antiparticle pair or an additional gluon, and that should be a correction to a simple one-gluon exchange. They could create additional pairs or gluons, which would be higher-order corrections.
We call this approach taking a perturbative expansion in quantum field theory, with the idea that calculating higher and higher-order contributions will give us a more accurate result.
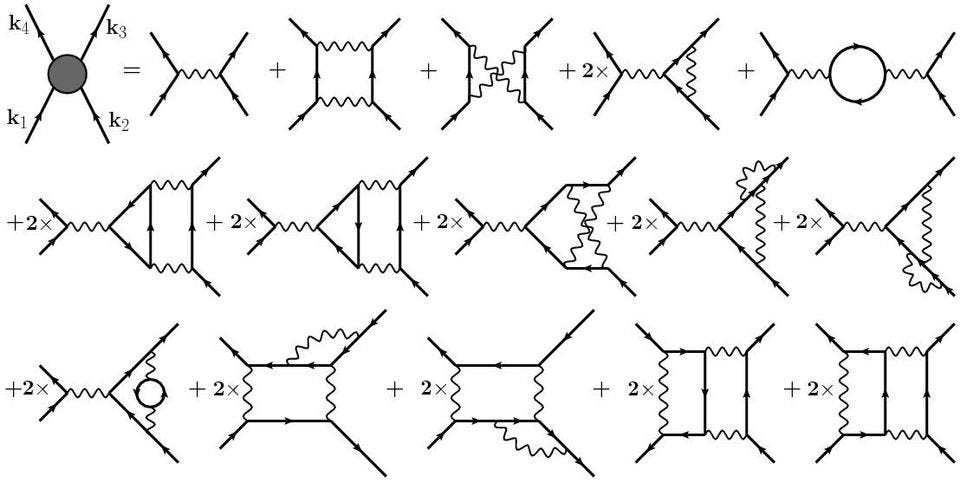
But this approach, which works so well for quantum electrodynamics (QED), fails spectacularly for QCD. The strong force works differently, and so these corrections get very large very quickly. Adding more terms, instead of converging towards the correct answer, diverges and takes you away from it.
Fortunately, there is another way to approach the problem: non-perturbatively, using a technique called Lattice QCD. By treating space and time as a grid (or lattice of points) rather than a continuum, where the lattice is arbitrarily large and the spacing is arbitrarily small, you overcome this problem in a clever way. Whereas in standard, perturbative QCD, the continuous nature of space means that you lose the ability to calculate interaction strengths at small distances, the lattice approach means there’s a cutoff at the size of the lattice spacing. Quarks exist at the intersections of grid lines; gluons exist along the links connecting grid points.
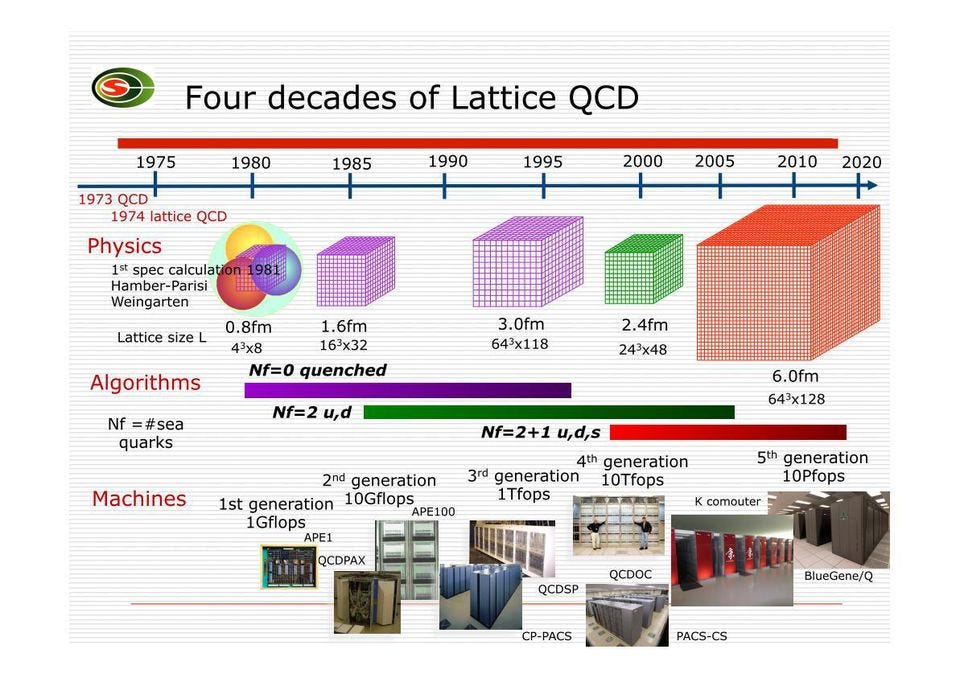
So long as you have enough computing power, you can recover the predictions of QCD to whatever precision you like, simply by making the lattice spacing smaller, which costs more in terms of computational power but improves your calculational accuracy. Over the past three decades, this technique has led to an explosion of solid predictions, including the masses of light nuclei and the reaction rates of fusion under specific temperature and energy conditions. The mass of the proton, from first principles, can now be theoretically predicted to within 2%.
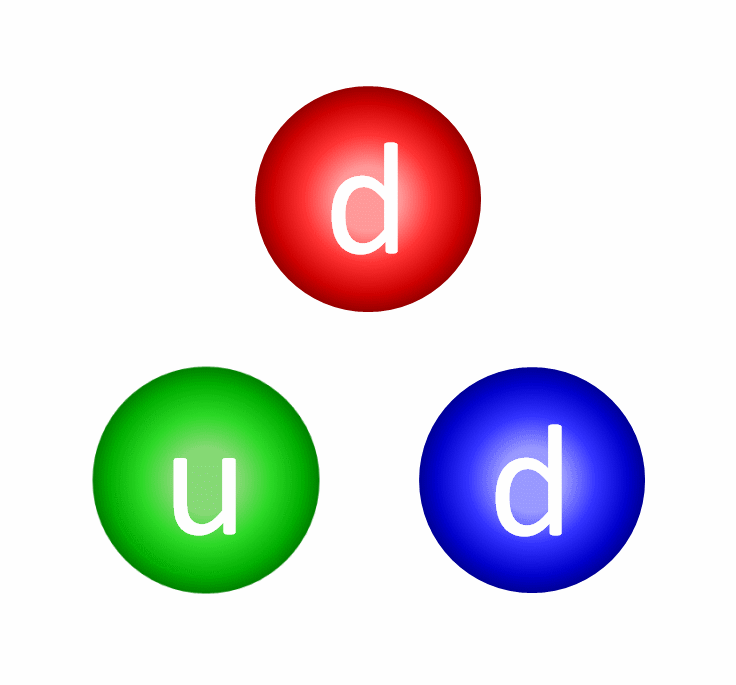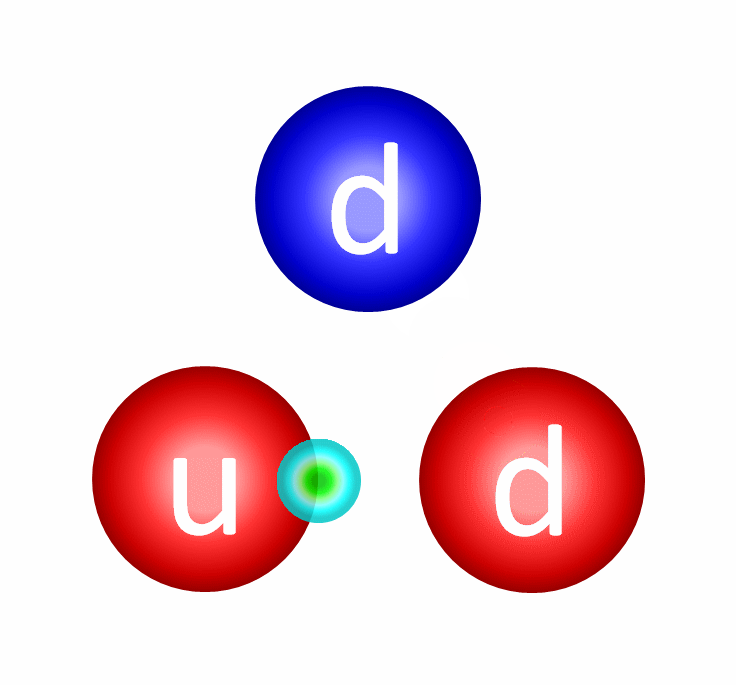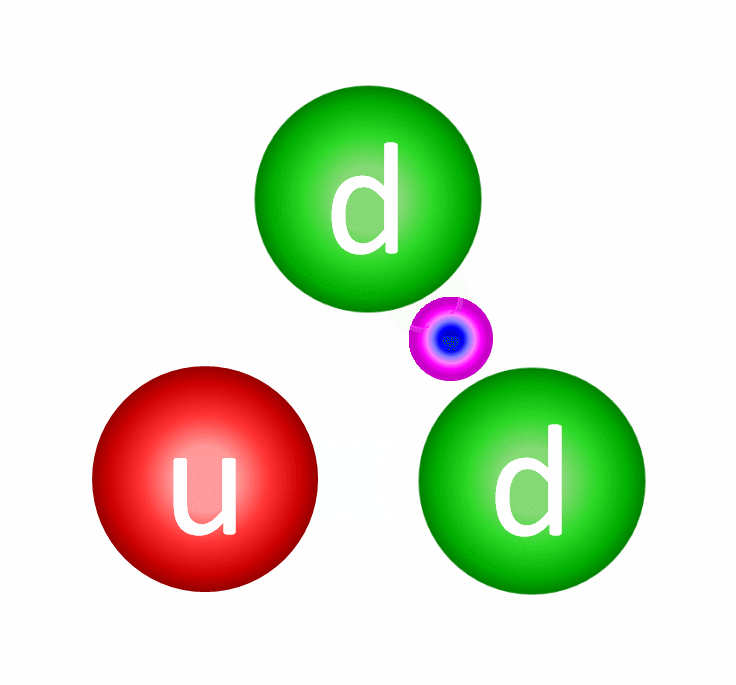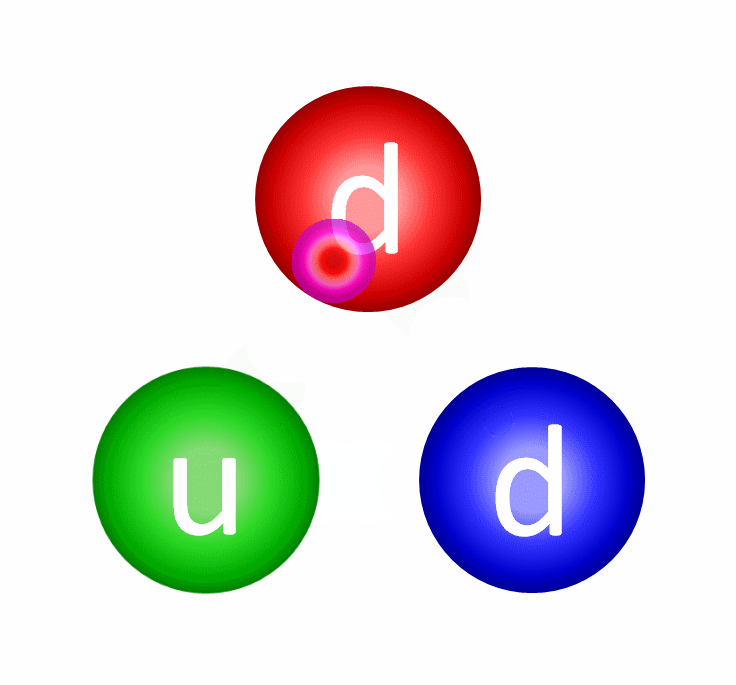
Lattice QCD is not only teaching us how the strong interactions lead to the overwhelming majority of the mass of normal matter in our Universe, but holds the potential to teach us about all sorts of other phenomena, from nuclear reactions to dark matter.
Later today, November 7th, physics professor Phiala Shanahan will be delivering a public lecture from Perimeter Institute, and we’ll be live-blogging it right here at 7 PM ET / 4 PM PT. You can watch the talk right here, and follow along with my commentary below. Shanahan is an expert in theoretical nuclear and particle physics and specializes in supercomputer work involving QCD, and I’m so curious what else she has to say.
Source: Medium.com





























Leave a Comment
You must be logged in to post a comment.